论文标题：Mechanical Foundations of the Generalized Second Law and the Irreversibility Principle

论文链接：https://www.mdpi.com/2673-9321/4/4/37

期刊名：Foundations

期刊主页：https://www.mdpi.com/journal/foundations

本文遵循玻尔兹曼-克劳修斯-麦克斯韦（Boltzmann-Clausius-Maxwell, BCM）理论框架，构建适用于任意尺度系统（包括单粒子系统——正如我们的范例所示）的广义第二定律（Generalized Second Law, GSL）。该定律超越了经典孤立系统熵增的第二定律（Second Law, SL），其本质是分析力学中机械平衡原理（稳定或不稳定，Mechanical Equilibrium Principle, Mec-EQ-P）与热力学第一定律的必然推论。我们提出了一种普适的不可逆性原理，涵盖所有自发或非自发过程，并适用于通过（dQ/dS）E定义的具有正负非平衡温度T的系统。与经典热力学采用的研究路径相反，我们通过逆向推导确立了GSL/SL，并明确了自发过程的判定标准：当T>0时，dS≥0；当T<0时，dS<0。值得注意的是，GSL/SL不适用于非自发过程（如内部约束的建立）。我们的研究证实，机械平衡原理是控制自发过程的根本机制，且温度（无论正负）必须被视为耗散过程的内在组成部分。

研究过程与结果

我们已准备好基于玻尔兹曼-克劳修斯-麦克斯韦（BCM）理论框架，通过聚焦孤立系统来总结我们对不可逆性的全新理解、经典第二定律（SL）成立所需的条件，以及导致其失效的机制。这一研究路径的直接成果是：我们推导出适用于任意尺度系统的广义第二定律（GSL），其适用范围突破了经典第二定律的局限。下文将重点阐述我们的核心发现，并探讨其令人瞩目的理论推论。

不可逆宏观热Td÷S_Q必须从Td÷S中扣除的观察结果，与我们在方程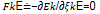,及其讨论中得出的前序结论一致。然而，方程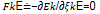,蕴含着更深刻的物理意义：尽管变量的变化会引发不可逆熵产生d_is_Q，但它既不会产生任何国际单位制（SI）下的微观功d_iW_k^E，也不会导致任何宏观尺度上的能量耗散。