论文标题：Image Encryption Scheme Based on Newly Designed Chaotic Map and Parallel DNA Coding

论文链接：https://doi.org/10.3390/math11010231

期刊名：Mathematics

期刊主页：https://www.mdpi.com/journal/mathematics

本文引用信息

Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. Image Encryption Scheme Based on Newly Designed Chaotic Map and Parallel DNA Coding. Mathematics 2023, 11, 231. https://doi.org/10.3390/math11010231

一、文章亮点介绍：

1. 提出了一种新的一维混沌系统模型，该系统能够在非常大的参数区间出现连续的强混沌特性，与传统一维混沌映射相比，该系统的优点是系统分岔图对应的混沌参数区间不存在周期窗口。

2. 提出了一种基于并行DNA编码和解码的快速图像加密算法。

3. 通过一系列复杂性准则证明了混沌系统模型的复杂混沌特性，并通过大量实验和安全性分析验证了所提出的图像加密方案的安全性。

二、文章介绍：

1.研究背景及目的

自非线性系统中发现混沌现象以来，混沌研究已成为非线性科学的核心内容之一，并引起了众多领域研究者的强烈关注。混沌信号的特性与密码学所需的属性有许多相似之处，如混沌信号的伪随机性、对初始条件和系统参数的极端敏感性以及高度复杂的非线性，这些都是密码学所急需的。这使得混沌系统近年来被广泛应用于构建密码系统。在图像加密方面，混沌密码学展现出明显的优势，并已成为混沌应用的主要领域。这归因于以下两个原因：一方面，图像信息数据量大、相关性较强且冗余度高，传统密码算法加密图像效率低下，时间成本特别高。另一方面，图像信息是使用非常广泛的视觉信息——人类获取的信息中有80%来自视觉。因此，图像信息加密尤为重要。于是，基于混沌和混沌安全通信的密码学研究方向应运而生。随着混沌密码学的发展，许多基于混沌的图像加密算法被提出。此外，设计具有更好性能的新型混沌系统模型也是混沌应用领域的一个热门研究话题。自阿德曼提出DNA计算以来，DNA计算技术受到了研究人员的广泛关注。近年来，基于DNA编码的信息加密技术也被引入图像加密领域，并提出了许多结合混沌和DNA编码的图像加密算法；但基于DNA编码的图像加密算法存在的一个缺陷就是加密算法的时间开销较大。

基于上述研究背景，本文设计了一种新型的一维分数形式的混沌映射，并提出了一种基于并行DNA编码的新型图像加密方案。其目的在于如下二个方面，一是提高混沌系统的混沌性能，从而提高系统带来的图像加密系统的安全性；二是提高基于DNA编码的信息加密算法速度。

2.模型及结果分析

本文提出新型一维（1D）混沌映射系统具有建构简单的特点，其数学模型由下列公式（1）描述

（1）

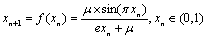
其中，μ和e是系统的控制参数。论文已证明，当参数μ和e满足下列式（2）所示的关系时，系统（1）是混沌的：

（2）

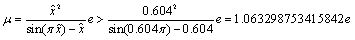
刻画系统的性能的几种图形如图1所示：

(a) 混沌系统（1）的分岔图 (b) 混沌系统（1）的Lyapunov指数曲线图

(c) 混沌系统（1）的时间序列图 (d) 混沌系统（1）蛛网图

图1.系统（1）的性能分析图

本文的图像加密算法整体框图如图2所示：

图2.图像加密算法的整体框图

本文的图像加密算法效果如图3所示：

(a)	(b)	(c)	(d)
(e)	(f)	(g)	(h)

图3. 加密算法的效果图.

(a)明文图像Baboon.(b)图(a)的直方图.(c)Baboon的加密图像.(d)图(c)的直方图.(e)明文图像Peppers. (f)图(e)的直方图.(g)Peppers的加密图像.(h)图(g)的直方图.

表1是本文算法与参考文献加密算法在相同软硬件环境下的时间开销对比。

表2. 加密/解密一幅256×256大小的灰度图像所需的时间对比(单位:秒).

3.讨论与总结

本文构造了一种新的一维分数型混沌映射系统模型，并利用该混沌系统设计了一种基于并行DNA编码的图像加密算法。对于这种新型混沌系统，文中采用了一系列混沌性能指标来证明其具有良好的混沌特性。与传统的一维混沌系统相比，该新型混沌系统具有更大的混沌参数范围和更复杂的混沌行为。针对基于DNA编码的图像加密算法耗时长的缺点，本文提出了一种基于并行DNA编码的图像加密算法。并行计算可以显著提高加密和解密算法的速度。该密码系统的初始密钥被设计为与明文图像的SHA-3哈希值相关联，从而使算法能够抵抗选择明文攻击。仿真实验和安全性分析结果表明，所提出的图像加密方案具有更好的加密性能和更少的时间开销，并且对噪声和数据丢失攻击具有很强的鲁棒性，这表明所提出的图像加密方案在安全通信应用中具有良好的应用潜力。

三、获奖采访：

请问您能向读者简单介绍一下自己吗？能否介绍一下您目前的研究方向和最新进展？

能。详情参见第四部分的作者介绍

请问您在Mathematics投稿的体验如何？是什么吸引了您选择Mathematics期刊？

我们在Mathematics投稿的体验非常满意。是下列因素吸引了我们选择Mathematics期刊：一是Mathematics具有较高的显示度，在JCR分区中被列入Q1分区。二是Mathematics期刊的主题范围广，尤其是“Chaos-Based Secure Communication and Cryptography”专刊的研究主题与我们的研究主题非常对口。三是Mathematics期刊的审稿效率极高，研究成果能够得到快速发表。

您认为在未来几年，哪些研究课题会成为研究界的最感兴趣的话题？

在未来几年，我们认为，与人工智能、大数据、信息安全相关的数学模型构建以及模型性能的评估、模型性能的可证明性研究会成为研究界的最感兴趣的话题。

对于希望在各自领域产生有意义影响的有抱负的年轻研究人员，您有什么建议吗？

建议年轻研究人员一定要把数学基础打好打牢，重视数学在各个领域的基础性作用，善于将数学应用于各自的工作领域。不管从事什么工作和研究，都要做到将理论与实践相结合。

作为奖项的获得者，请问您有什么感想？

作为奖项的获得者，感想非常丰富。在众多的论文之中，本文能够得到广大读者的高度关注和认可，既感觉自己非常荣幸，也提高了我们对科研的自信心，同时觉得研究非线性系统的建模、性能分析及其在信息安全领域的应用是非常有意义的工作。

四、作者介绍

朱身力

湖南大学网络空间安全学院

研究方向：图像加密、信息隐藏。

邓晓衡

中南大学电子信息学院

研究方向：无线网络、边缘计算、物联网、大数据、人工智能与通信安全技术。

张文东

新疆大学软件学院

研究方向：群智感知、人工智能（图像处理）、信息安全技术。

朱从旭

中南大学计算机学院

研究方向：非线性混沌系统的建模与分析、混沌密码学、图像加密

中南大学邓晓衡研究团队介绍

学术成果：在包括IEEE TON, TMC, TDSC, TKDE, TITS, TVT, IOT, TNSE, 计算机学报，计算机研究与发展，电子学报，通信学报以及IEEE CVPR，ICASSP，ICC，Globecom, WCNC, ICTAI，IPCCC等国内外权威的刊物与国际会议上发表与研究论文150余篇。

科研项目：主持和参加包括国家自然科学基金、国家“863”计划课题、教育部重点项目、教育部高等学校博士点专项基金、湖南省自然科学基金、湖南省科技计划项目以及大型企业信息化项目等分布式信息系统研制等纵横向科研项目30余项。

学术兼职：邓晓衡教授，现为中南大学电子信息学院院长，湖南省数据传感与交换设备工程中心主任, 湖南省“芙蓉学者”特聘教授，湖南省计算学会常务理事、湖南省电子学会副理事长，CCF杰出会员，IEEE高级会员，CCF长沙执委，曾任CCF YOCSEF 2009-2010年度长沙主席。

五、Mathematics 期刊及期刊活动介绍

1. 期刊介绍

主编：Francisco Chiclana, School of Computer Science and Informatics, De Montfort University, UK

Mathematics (ISSN 2227-7390) 是一个专注于数学领域的国际开放获取同行评审期刊，涵盖纯数学和应用数学的各个领域。自2013年创刊以来，Mathematics 期刊发展迅速，其于2015年被ESCI数据库收录，于2017年被Scopus数据库收录，2018年被SCIE数据库收录，期刊最新影响因子为2.2，JCR位列Q1，排名29/483；最新CiteScore为4.6，在“General Mathematics”类别位列Q1。

Mathematics 涵盖纯数学和应用数学的各个领域。重点发表代数与逻辑、几何与拓扑、数学分析、统计与运筹学、应用数学，包括数学与计算机科学、控制理论与力学、数学生物学、数学物理、金融数学等数学在其他各学科应用的文章。期刊致力于为研究者提供一个高质量高效率的学术交流平台。目前投稿至首次决定的时间中位数为18.4天，从接受稿件到正式发表，时间中位数为2.4天。

期刊在国内100多位编委 (学者名单详见：https://www.mdpi.com/journal/mathematics/editors?search=china) 及其他全球700多位学编的支持下，秉承着开放获取的理念，确保发表的研究成果可被全球学者免费获取，加速科研成果的传播和影响力。

2. 期刊奖项及会议

•2025年青年学者奖 (2025 Young Investigator Award)

旨在表彰在数学领域做出卓越研究成果的青年研究者

奖项奖金：2000瑞士法郎；

免费发文：可在2026年12月31日前经同行评审后在Mathematics 期刊免费发表一篇论文 (文章类型：article/review)；

荣誉证书。

提名截止时间：2025年12月31日。

详见：https://www.mdpi.com/journal/mathematics/awards/3395

•第二届国际数学与应用在线会议 (IOCMA2026)

由MDPI期刊Mathematics 主办的第二届国际数学与应用在线会议 (The 2nd International Online Conference on Mathematics and Applications, IOCMA2026) 将于2026年6月10日至12日在线举行，本次活动免费对全球数学及应用数学领域所有学者开放。会议将开放口头报告和海报展示，并设立多项学术奖项，以鼓励优秀研究成果。获奖者将有机会获得200瑞士法郎的奖金及在Mathematics 期刊上优惠发表论文的机会。欢迎全球数学及相关领域的研究人员、专家学者踊跃投稿并参与会议。

摘要投稿截止日期：2026年2月10日；

注册截止日期：2026年6月5日。

详见：https://sciforum.net/event/IOCMA2026

欢迎广大数学领域的学者投稿与合作，共同推动数学研究的发展与创新。