论文标题：Synchronization of Fractional-Order Delayed Neural Networks Using Dynamic-Free Adaptive Sliding Mode Control

论文链接：https://doi.org/10.3390/fractalfract7090682

期刊名：Fractal Fract

期刊主页：https://www.mdpi.com/journal/fractalfract

研究背景

分数阶延迟神经网络（FONNS）因其长记忆效应和非线性动力学特性，在安全通信、生物医学建模等领域展现独特优势，但系统中的时间延迟、参数不确定性及输入饱和问题，导致传统同步控制方法面临收敛速度慢、鲁棒性不足的挑战。现有研究多依赖系统动态模型，难以适应异同网络的复杂场景。广州大学与丹麦奥胡斯大学团队提出基于频率分布模型（FDM）与分数阶Lyapunov稳定性理论的动态-自由自适应滑模控制（adaptive-SMC）方法，实现无需系统动态信息的高精度同步控制。

核心方法与创新突破

研究团队设计了一种无需系统动态信息的智能控制框架，其核心创新体现在三方面：

1. 动态解耦控制机制：通过构建平滑滑动面

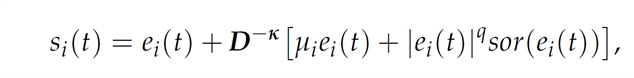
将分数阶系统的同步误差动态转化为可追踪的稳定轨迹，避免了传统方法对系统线性/非线性项的依赖。该滑动面设计如同 “智能导航路径”，引导系统状态误差快速收敛至零，实验显示二维 Hopfield 网络的同步误差在短时间快速趋于稳定。

2. 自适应抗干扰策略：引入实时参数更新机制，可自动估计系统不确定性边界，结合输入饱和处理函数，有效抑制硬件传输限制导致的控制失效。如下图所示，在三维系统中，即使分数阶数发生偏移（如 κ=0.96），该方法仍能保持轨迹同步。

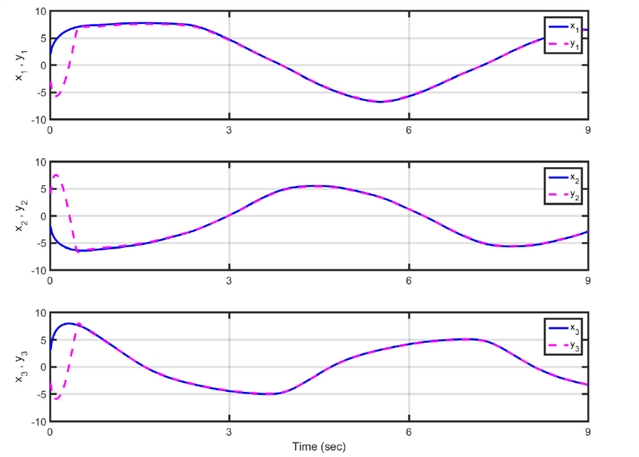
Hopfield延迟FONNSs同步的时间演化

研究成果与应用价值

1.理论层面：首次建立无需系统动态信息的 FONNS 同步稳定性判据，拓展了分数阶 Lyapunov 理论的应用边界，相关成果为混沌系统控制提供了普适性框架。

2.工程应用：本项研究在需要同步系统的各个领域都具有潜在的应用前景。为混沌系统稳定同步至关重要的各个领域的研究和应用开辟了新的可能性。

Fractal and Fractional 期刊介绍

主编：Carlo Cattani, University of Tuscia, Italy

期刊研究范围包括分形和分数阶微积分基础研究及其在不同科学和工程领域中的应用。