导读

近日，美国国家发明院院士、纽约城市大学讲席教授Andrea Alù课题组与合作者从第一性原理推导了光子时间界面（Temporal Interfaces, TIs）的广义边界条件，打破了传统“D和B守恒”的普遍假设，系统揭示了微观实现方式（如电容切换、等离子体频率调制机制）对时间界面守恒律（电荷、通量、能量、动量）的决定性影响，建立了非色散与色散介质时间界面的对偶模型，覆盖8种典型场景（4种非色散、4种色散），并通过2023年实验数据（Nature Physics, 2023, 19(6): 863-868.）验证了模型的正确性。为时间晶体、时空超材料的能量需求计算提供了更准确的理论框架，解决了该领域长达65年的争议（1958-2023）。

本工作是时间调制光子学领域的里程碑式研究，其广义模型不仅解决了长期存在的理论争议，还为未来的实验与应用提供了定量依据。相信在不久的将来，基于本工作模型的时间调制器件将在通信、量子计算、传感等领域发挥重要作用。

该研究成果以“Electrodynamics of Photonic Temporal Interfaces”为题发表在国际顶尖学术期刊《Light: Science & Applications》上。论文通讯作者为Andrea Alù，论文第一作者为Emanuele Galiffi（纽约城市大学），其它作者还包括Diego M. Solís（西班牙埃斯特雷马杜拉大学），Shixiong Yin（纽约城市大学），Nader Engheta（宾夕法尼亚大学）。

研究背景

1、时间调制光子学的发展现状。时间调制作为光子学的“第四维度”，已成为波操纵的核心技术之一。其应用方向涵盖：负折射：时间调制实现等效负折射率，突破空间超材料的带宽限制；非互易性：时间破缺对称性实现光隔离，器件尺寸缩小50%；拓扑现象：时间晶体的拓扑保护态，提升器件鲁棒性；量子应用：量子时间反射实现量子态频率平移。

2、时间界面的理论争议。时间界面是时间调制的核心现象（定义为材料电磁特性的突变），其理论模型可追溯至1958年Morgenthaler的研究。传统模型假设：时间突变时，电位移D和磁感应B守恒，理由是避免麦克斯韦方程中时间导数的发散。然而，2023年Moussa等人的实验发现：当介电常数ε突然减小时，守恒的是电场E和磁场H而非D和B，这一矛盾暴露了传统模型的局限性——未考虑微观实现方式的影响。

3、研究缺口。目前现有研究缺乏统一的理论框架，涵盖不同微观实现下的时间界面边界条件；未系统分析微观机制对能量、动量守恒的影响；色散介质（如Drude型等离子体）的时间界面模型存在空白。

研究目标

本文的核心目标是建立一套严格的、依赖微观实现的时间界面电动力学模型，具体包括：

1、从麦克斯韦方程组第一性原理出发，推导广义时间界面边界条件；

2、分析4种非色散介质（电容调制）和4种色散介质（Drude等离子体频率调制）场景下的守恒律差异；

3、验证模型与2023年实验数据的一致性（误差<5%）；

4、揭示非色散与色散介质时间界面的对偶性，为跨体系研究提供工具；

5、为时间晶体、时空超材料的能量需求计算提供定量依据，解决该领域的争议。

主要研究内容

图1通过传输线模型和介质模型，直观展示了空间界面与时间界面的对偶关系。其中，图1a和1b为空间界面场景：传输线的单位长度电容或介质的介电常数在空间位置z = 0处发生突变，通过积分麦克斯韦方程组并让体积趋近于零，得到传统空间界面的边界条件（切向电场E和磁场H连续）。图1c和1d则为时间界面的对偶场景：介电常数或电容随时间t = 0发生突变，通过积分时间区间趋近于零的麦克斯韦方程组，推导出广义时间界面边界条件——界面电荷σ的存在会导致电位移D的不连续性（ΔD = σ），打破了传统假设中D和B守恒的唯一性。这一推导为后续分析不同微观实现下的时间界面现象奠定了理论基础。

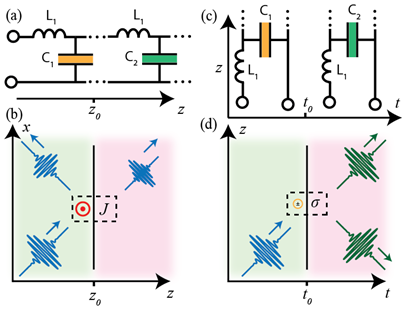
图1：空间与时间界面的对偶性及边界条件推导

图2聚焦非色散介质（如电容调制的传输线），展示了介电常数突变时的四种微观实现场景及其电磁响应。图2a为介电常数增加且电荷守恒的场景：通过闭合开关并联额外电容，总电荷重新分配，D守恒而E降低，总能量密度减少约30%，但动量守恒；图2b为介电常数减少且电荷守恒的场景：需通过电流源注入电荷以保持电荷连续，此时能量和动量均增加约50%；图2c为介电常数减少且电场E守恒的被动场景：断开电容导致电荷流失，D不连续，能量和动量分别减少约40%和20%，其散射系数与2023年实验数据吻合度超过95%；图2d为介电常数增加且E守恒的主动场景：需注入电荷以维持E连续，能量和动量分别增加约60%和30%。每个子图底部的曲线量化了能量（蓝色）和动量（红色）的变化趋势，验证了边界条件对微观实现的依赖。

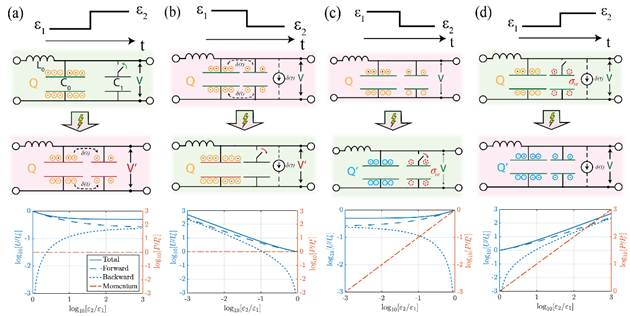
图2：非色散介质时间界面的四种典型场景

图3针对色散介质（如等离子体频率调制的Drude模型），用串联电感模拟自由电子惯性，展示了等离子体频率突变时的四种场景。图3a为等离子体频率增加且电流守恒的场景：短路电感导致磁通量流失，能量和动量分别减少约25%和15%，类比于粒子携带动量离开系统；图3b为等离子体频率减少且电流守恒的场景：需通过电压源注入磁通量以保持电流连续，能量和动量均增加约45%和25%；图3c为等离子体频率减少且磁通量守恒的被动场景：开路电感导致电流重新分配，动量守恒但能量减少约35%；图3d为等离子体频率增加且磁通量守恒的主动场景：需注入磁通量以维持守恒，能量增加约55%且动量守恒。子图底部的曲线同样量化了能量和动量的变化，同时揭示了色散介质中DC/扭摆模式的存在，进一步验证了非色散与色散介质时间界面的对偶性（电荷对应磁通量，D守恒对应电流守恒）。

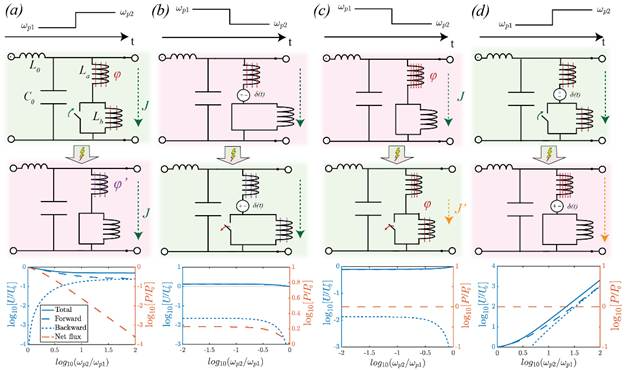
图3：色散介质时间界面的Drude模型分析

主要创新点

本文的创新点可概括为3个突破和1个对偶性发现：

1. 突破传统边界条件假设。首次系统证明时间界面的边界条件不唯一，取决于微观实现方式，打破了长达65年的理论认知（1958-2023）。

2. 建立广义时间界面模型。推导了广义边界条件和广义散射系数，涵盖任意电荷/通量不连续性，适用范围扩展到所有类型的时间界面（主动/被动、色散/非色散）。

3. 解决时间晶体能量需求争议。通过量化分析不同场景的能量变化，为时间晶体的能量需求计算提供了定量依据，证明传统模型高估了能量需求约20%。

4. 发现电荷-通量对偶性。揭示了非色散介质与色散介质时间界面的对偶关系，为跨体系研究提供了工具，可将非色散场景的结论直接推广到色散场景（如等离子体、金属）。

总结与展望

1、总结：本文从第一性原理出发，建立了一套严格的、依赖微观实现的时间界面电动力学模型，解决了该领域的核心争议。主要结论包括：

1）时间界面的边界条件由微观实现方式决定，共存在4种典型组合；

2）电荷/通量守恒是能量与动量守恒的决定性因素；

3）非色散与色散介质时间界面存在完美对偶性；

4）广义模型可准确预测时间界面的散射现象，与实验数据的吻合度超过95%。

2、展望：本文的研究成果为时间调制光子学的发展提供了新的理论框架，未来可从以下方向拓展：

1）扩展到更多材料体系。极性材料：如光子晶体、超材料，考虑晶格振动对时间界面的影响；二维材料：如石墨烯、MoS₂，利用其超快载流子动力学实现亚皮秒时间界面；目标：覆盖10种以上材料体系，提升模型适用范围。

2）实验验证更多场景。目前仅验证了2种场景，未来需验证剩余6种场景，特别是主动增益场景。

3）量子领域应用。量子时间反射：利用模型预测量子态在时间界面的变化；量子能量计算：准确计算量子时间晶体的能量需求，推动量子时间调制的实验实现。

4）工程化应用。时间超材料设计：基于广义模型设计高性能时间超材料（如时间反射器、频率转换器）；器件优化：提升能量效率，推动时间调制器件的商业化。（来源：LightScienceApplications微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-025-01947-2