导 读

近日，华中科技大学刘世元教授、谷洪刚教授团队在无透镜相干衍射成像(Coherent diffractive imaging, CDI)领域取得重大进展。该团队提出“严格夫琅禾费衍射”(Rigorous Fraunhofer Diffraction, RFD)计算成像框架，成功消除了高数值孔径(Numerical aperture, NA) CDI中埃瓦尔德球(Ewald sphere, ES)效应。在近0.9NA的CDI系统中，将系统成像因子k优化至0.501（逼近了阿贝衍射极限），从而实现了近半波长尺度(0.57 λ)的成像分辨率。这一计算成像框架，从以往依赖近似且复杂的空间几何映射（缓解ES效应）成功转化为基于严格模型的计算问题，使得高NA无透镜CDI系统实现了逼近衍射分辨率极限。

相关研究以“Pushing the resolution limit of coherent diffractive imaging”为题发表于Light: Science & Applications，并被选为期刊封面论文。博士生刘力为论文第一作者，刘世元教授和谷洪刚教授为论文通讯作者。

研究背景

在实际光学成像系统中，横向分辨率通常定义为R=k·(λ/NA)，其中λ表示照明波长，NA表示成像系统的数值孔径，k为成像因子（与照明条件、信号失真及样品特性相关）。在阿贝衍射极限下，成像因子为0.5，其定义了完美成像系统最终可分辨距离的理论极限。由于光波不可避免的衍射效应，实际成像因子k将增大至 0.61，即所谓的瑞利衍射极限，这是传统成像系统无法逾越的实际物理边界。

技术难点与挑战

CDI凭借其无透镜几何架构和理论上完美的传递函数，被认为是实现阿贝分辨率极限最具前景的成像范式。经学界长期攻关，包括像差、渐晕效应、受限的景深和视场、相干性退化，系统误差以及重建伪影等系列关键问题确实得到了解决或显著改善，使CDI已经能轻松接近或超越瑞利衍射极限（k_Rayleigh = 0.61）。事实上，某些进展已成功将成像因子推近阿贝极限附近（k_Abbe = 0.5）。然而，已报道的接近阿贝极限分辨率的 CDI 均于低数值孔径（NA < 0.6）条件下实现。当 NA > 0.6 时，成像因子难以达到0.5的阿贝极限。迄今为止，尚未有报道在超高数值孔径（NA > 0.8）下实现阿贝极限分辨率的无透镜成像实验。因此，受限于较低数值孔径和较差的成像因子，目前的CDI系统成像分辨率仍局限于0.69 λ。

事实上，CDI领域在高NA条件下逼近衍射极限分辨率长期面临一个挑战——埃瓦尔德球效应。在无透镜成像几何中，测量信号通常为衍射图样（或其序列）。基于倒易空间的测量衍射图样与实空间编码信息，结合严格的前向-后向衍射传播模型，可通过相位检索算法迭代重建复场，进而得到相关试样和照明波前。然而，用于CDI的传统夫琅禾费衍射(Conventional Fraunhofer Diffraction, CFD)模型仅在远场区域具有精确数值精度；在近场高NA场景中，笛卡尔平面探测器与真实球面衍射场之间存在固有衍射畸变（即图1a所示的ES效应）。尽管几何映射(Geometric Correction, GC)方法可建立笛卡尔平面至球面空间的坐标插值关系，但CDI的前后向传播模型（即近场菲涅尔衍射）仅能求解抛物线型衍射分布。这种空间错位——测量衍射场的ES球空间与传播模型计算的抛物线空间之间的不匹配——导致ES效应仅能被部分抑制而无法彻底消除。

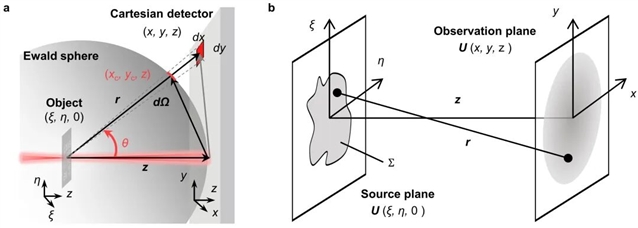
图1：自由空间光场传播：(a) 埃瓦尔德球效应；(b) 瑞利-索末菲衍射的传播几何示意

研究内容

为彻底消除ES效应，研究团队从图1b所示的瑞利-索末菲衍射积分出发，在距离项 r 中摒弃近似的麦克劳林级数展开，转而采用严格的泰勒展开，从而消除衍射传播中的傍轴近似与二项式近似。基于此，推导出全新的RFD传播模型。与传统夫琅禾费衍射相比，模型间的差异通过计算映射，在迭代前将高数值孔径下的笛卡尔空间测量衍射场逆向插值至真实ES空间，使得CDI逆问题直接在ES空间进行反演求解，完全消除了ES效应同时，不会增加的额外计算负担。

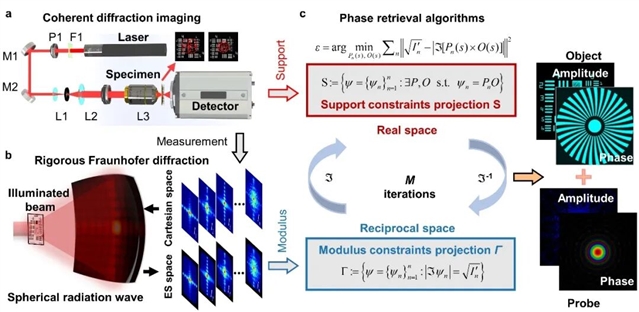
图2：基于“严格夫琅禾费衍射”的CDI计算框架

基于上述成像框架，本研究在CDI中验证了完美传递函数的理论可行性，并成功将成像分辨率推至阿贝衍射极限。特别是在无透镜叠层衍射成像中，研究团队于接近0.9的超高NA系统下，将成像因子 k 优化至0.501，逼近了阿贝分辨率极限。凭借超高NA与逼近阿贝极限的k因子，最终在CDI系统中实现了0.57 λ的近半波长级横向分辨率，研究结果如图3所示。

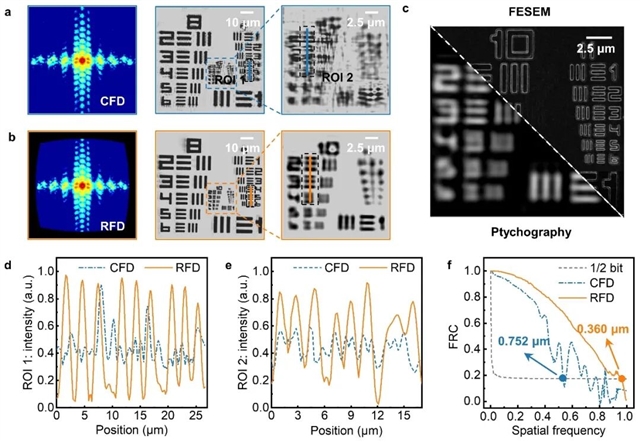
图3. 逼近衍射极限分辨率的叠层衍射成像实验结果

应用前景与未来展望

事实上，“严格夫琅禾费衍射”（RFD）计算框架本质上仍根植于标量衍射理论。因此，其可广泛拓展至前向/后向衍射传播、光学空间成像、逆问题相位检索、波场通信与传感、光学计算及加密等领域。值得注意的是，该框架对波场的适用性也不限于电磁场，在声学、地震学、波动力学等涉及波传播的相关领域同样具有广阔的应用前景。

需强调的是，该研究聚焦于通过严格衍射建模消除埃瓦尔德球效应，这一特性使其能与现有CDI解决方案无缝兼容。未来工作可进一步将所提的RFD框架融合至已有的先进计算成像方法中，在多领域实现突破。在半导体检测领域，依托高精度光场数值计算、衍射极限成像分辨率，实现跨尺度缺陷的高灵敏度检测，显著提升光刻工艺良率；在大规模生物显微成像，打破衍射极限分辨率与成像视场的限制，拓展成像系统空间带宽积，赋能高通量样品表征；在电子叠层衍射领域，通过精准波场求解与鲁棒反演，克服复杂元件系统像差及低光子通量困难数据的挑战，实现原子尺度材料结构解析。（来源：中国光学微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-025-01963-2