论文标题：Solitary Wave Solutions to a Fractional Model Using the Improved Modified Extended Tanh-Function Method

论文链接：https://doi.org/10.3390/fractalfract7030252

期刊名：Fractal Fract

期刊主页：https://www.mdpi.com/journal/fractalfract

研究背景

非线性分数阶偏微分方程（NLFPDEs）是描述物理、工程和流体动力学等领域中复杂现象的重要工具。NLFPDEs的孤立波解已经成为理解复杂现象的长期动态的重要工具。时空分数阶对称正则长波（SRLW）方程是该类方程中的一个典型模型，在模拟浅水波、等离子体中的离子声波和空间电荷波等方面具有广泛应用。Taibah大学的学者Mohammed Bakheet Almatrafi 通过应用改进扩展的 tanh 函数方法，结合 Jumarie 的修正Riemann-Liouville导数处理SRLW方程中的分数阶导数，为读者展示了获取 SRLW 方程多种形式（三角、双曲、有理函数等）行波解的思路，为求解其他 NLFPDEs 提供了新思路。

核心方法与创新点

本研究的核心是采用改进的修正扩展tanh函数法，并结合Jumarie修正的Riemann-Liouville导数来处理分数阶算子。

方法的创新点体现在：

1. ：通过分数阶复变换 ，将原分数阶方程转化为常微分方程（ODE）。

2. 通过该方法呈现行进波解为 ，其中辅助函数 G(ξ) 满足Riccati微分方程的解 

3. 通过系统性地讨论Riccati方程中参数 (a₀、a₁等)的不同情况，可推导出多种行波解，包括双曲函数、三角函数、有理函数解。

研究成果

研究发现，用改进的扩展 tanh 函数方法结合 Jumarie 修正Riemann-Liouville导数，得到 SRLW 方程的70个不同形式行波解，涵盖了孤子解、周期解等多种类型。

以下为若干代表性解的示例：

1. 在特定参数下（a₀=a₁=a₃=0, a₂>0, a₄<0），得到的行波解：

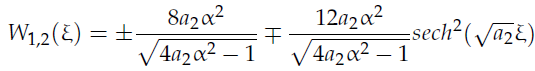
2. 在特定参数下（a₀=a₁=a₃=0, a₂<0, a₄>0），得到的行波解：

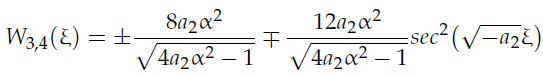
3. 在特定参数下（a₁=a₃=0, a₂<0, a₄＜0），得到的行波解：

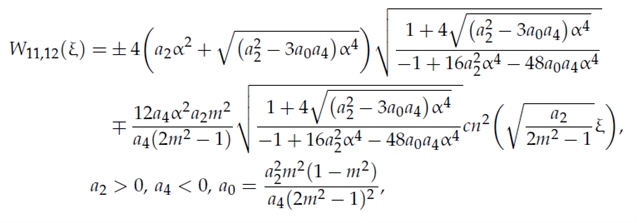
研究还直观展示了行波解的图形化行为。

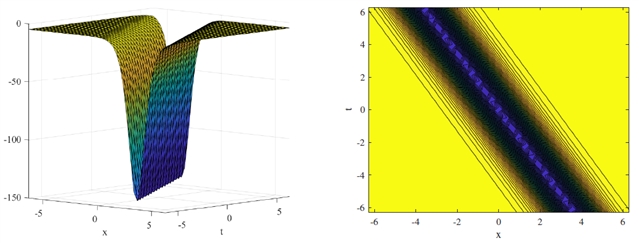
Fractal and Fractional 期刊介绍

主编：Carlo Cattani, University of Tuscia, Italy

期刊主题涵盖包括分形和分数阶微积分基础研究及其在不同科学和工程领域中的应用研究。现已被 SCIE (Web of Science)、Scopus 等重要数据库收录，JCR category rank: 22/136 (Q1)，中国科学院2区。