论文标题：Geometric phase opens new frontiers in nonlinear frequency conversion of light (几何相位为非线性光频转换开辟新前沿)

期刊：Frontiers of Physics

作者：Mai Tal, Danielle Ben Haim, Tal Ellenbogen

发表时间： 19 Nov 2021

DOI：10.1007/s11467-021-1123-4

微信链接：点击此处阅读微信文章

VIEW & PERSPECTIVE

Mai Tal, Danielle Ben Haim, and Tal Ellenbogen*, Geometric phase opens new frontiers in nonlinear frequency conversion of light, Frontiers of Physics 17(1), 12302 (2022)

REVIEW ARTICLE

Aviv Karnieli, Yongyao Li, and Ady Arie*, The geometric phase in nonlinear frequency conversion, Frontiers of Physics 17(1), 12301 (2022)

几何相位为非线性光频转换开辟新前沿

非线性光频转换涉及光子间通过材料非线性介电响应特性的相互作用并在新频率上产生光。其第一个实例是二次谐波产生(SHG)[1]：两个频率为?的入射光子在材料中结合并相干地发射一个频率为2?的光子。此后多种非线性光频转换过程，包括三波和四波混频以及高阶相互作用等被陆续验证[2]。自其实验验证和相关理论提出以来[3]，非线性光混频一直在推动相关技术进步和对新奇物理现象的探索。除了可以在从深紫外到太赫兹频率[4]的光学频率范围内产生相干的高强度光，非线性光混频也为光的控制提供了新的手段。目前该领域的前沿包括非线性全息光学[5, 6]、非互易系统的研究[7]以及为现代量子技术发展的光纠缠态的产生和操控等[8, 9]。

研究几何相位在非线性光混频过程中的作用是非线性光频转换中一个富有前景的子领域。Karnieli等人在最近的综述中对该领域的发展做了全面的回顾[10]。这一领域开创于30年前[11, 12]，现在引起了大量的研究关注，激发了对光频转换过程中基本问题的新见解，并提供了控制和利用非线性光混频动力学的新技术。

几何相位(Geometric Phase)的概念最早是由M. Berry提出的[13]，用来表示一个量子态在绝热演化时获得的相位，可形象理解为一个矢量平行于曲面运动时的旋转过程[14]。自提出以来，几何相位被推广到更一般的形式[15, 16]并在凝聚态物理和光学中得到了广泛应用。在光学领域中，尚有早于几何相位的类似概念[17]，如Pancharatnam在研究单色光偏振态之间的干涉时使用的Poincaré球面的几何表示[18]。随后的研究发现，Pancharatnam相位类似于量子力学系统含时演化时的几何相位[19, 20]。“Pancharatnam-Berry (PB)相位”被相应提出并在线性光学操控中获得了广泛应用。特别是在超表面材料中，PB相位被用于开发各种新的光学控制平面光学元件[21]。

几何相位在非线性光混频过程中主要有两方面的表现形式：第一种涉及频谱域变换时体材料中相互作用光波在传播过程获得的几何相位；第二种与偏振变换中伴随的几何相位有关，最常见的是与超表面的频率转换有关。

和频产生(SFG)的参数化过程是第一种形式（即几何相位在频谱域表现）的典型例子，可用Block球形象表示[22, 23]。光混频过程的几何表示及其与量子力学系统的类比，有助于提升对这一过程本质的理解并开发控制非线性相互作用的新手段[22, 24]。这种几何表示也推进了光频转换过程中伴随的几何相位的表述。例如，用调制QPM晶体中的SFG波动力学与磁场中自旋1/2粒子的动力学之间的类比 [23, 25]。此外，非线性光混频的几何表示和伴随的几何相位也激发了该领域的多种有趣进展。例如，几何表示通常被用于提高非线性转换的效率和改善对混频过程的控制；几何相位被用于非线性光束整形，其在非线性光混频中的非互易表现也有相关研究；体材料中一系列三波和四波混频过程中几何相位的计算；双折射晶体在光频转换过程中积累的几何相位；非线性人工规范场中传播时伴随的几何相位等。文献[10]详细阐述了该领域的发展和研究现状。

第二种情况对应光频转换过程中伴随偏振变换的几何相位。这种类型的几何相位可视为PB相的非线性延伸。非线性PB相主要集中在非线性光学超表面的研究中，相关的基于超薄的超表面材料的光学元件制备以及可控度高的光频转换过程引起了大量的研究关注[6, 26]。

超表面的非线性可能源于组成超原子的材料、表面、沉底以及结构设计等。这些材料或结构的非线性可以通过设计超原子来限制电磁场、通过等离子体和Mie共振、以及通过超表面上的协同效应来大大增强[27, 28]。因此，超原子的尺寸、形状、对称性和位置等设计参数对超表面的整体非线性响应和功能性起主要作用。

在超表面的光频转换过程中，相互作用的光波会累积一个非线性相位。由于超表面很薄，这一相位通常与超表面的复有效非线性磁化率而非传播有关。超原子取向的变化可以为相互作用的光波增加一个几何相位 [29-31]，如图右上所示。非线性PB相的这种表现形式为控制超表面的非线性响应和功能性提供了重要手段。例如，圆偏振光之间通过材料的相互作用和转换，要求自旋角动量守恒。此条件对与几何相位和材料(或超原子)对称性相关的过程设定了严格的选择规则[26, 32, 33]，因此超原子取向可连续变化的性质为获得非线性相互作用的连续相位控制提供了有用的工具。

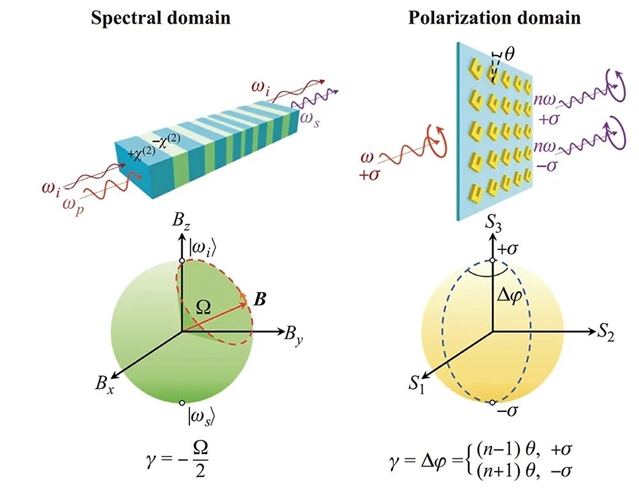
这一概念被用于各种光混频方案中，以控近红外和可见光区域的光波[26]，最近也用于太赫兹频段[34]。非线性几何相位超表面表现出各种先进的非线性功能，包括光束整形、成像、全息、图像编码和光束偏转，也被用于研究非线性光混频过程中的各种自旋角动量相互作用、控制非线性矢量场的产生等。参考文献[10]详细描述了该领域最激动人心的发展。

Berry和Pancharatnam总结出的几何相位概念，加深并扩展了对非线性光混频过程的理解和控制能力，在频谱域变换和偏振域变换中有诸多应用。在频谱域变换中，二次非线性晶体工程极化在最近的许多工作中发挥了主要作用；而对于偏振域变换，超表面的纳米加工能力起到了重要作用。未来随着非线性晶体三维极化技术[35]和非线性超材料的制备技术的发展，几何相位在频谱域和偏振域的结合将是一个新的热点，可能开启构建混合非线性超结构的研究。在这种结构中，频谱域和偏振域的几何相位都是可调的。这可能为大幅提升非线性光混频的转换效率以及在非线性光传播及其控制方面的基础研究开辟新的道路。

References

1. P. A. Franken, A. E. Hill, C. W. Peters, and G. Weinreich, Generation of optical harmonics, Phys. Rev. Lett. 7(4), 118 (1961)

2. R. W. Boyd, Nonlinear Optics, Elsevier, 2003

3. J. A. Armstrong, N. Bloembergen, J. Ducuing, and P. S. Pershan, Interactions between light waves in a nonlinear dielectric, Phys. Rev. 127(6), 1918 (1962)

4. E. Garmire, Nonlinear optics in daily life, Opt. Express 21(25), 30532 (2013)

5. A. Shapira, L. Naor, and A. Arie, Nonlinear optical holograms for spatial and spectral shaping of light waves, Sci. Bull. (Beijing) 60(16), 1403 (2015)

6. S. Keren-Zur, L. Michaeli, H. Suchowski, and T. Ellenbogen, Shaping light with nonlinear metasurfaces, Adv. Opt. Photonics 10(1), 309 (2018)

7. Z. Sun, Y. Yi, T. Song, G. Clark, B. Huang, Y. Shan, S. Wu, D. Huang, C. Gao, Z. Chen, M. McGuire, T. Cao, D. Xiao, W.T. Liu, W. Yao, X. Xu, and S. Wu, Giant nonreciprocal second-harmonic generation from antiferromagnetic bilayer CrI3, Nature 572(7770), 497 (2019)

8. J. Wang, F. Sciarrino, A. Laing, and M. G. Thompson, Integrated photonic quantum technologies, Nat. Photonics 14, 273 (2020)

9. J. Su, L. Cui, J. Li, Y. Liu, X. Li, and Z. Y. Ou, Versatile and precise quantum state engineering by using nonlinear interferometers, Opt. Express 27(15), 20479 (2019)

10. A. Karnieli, Y. Y. Li, and A. Arie, The geometric phase in nonlinear frequency conversion, Front. Phys. 17(1), 12301 (2021)

11. P. Mandel, P. Galatola, L. A. Lugiato, and W. Kaige, Berry phase analogies in nonlinear optics, Opt. Commun. 80(3-4), 262 (1991)

12. M. S. Alber, G. G. Luther, J. E. Marsden, and J. M. Robbins, Geometric phases, reduction and Lie-Poisson structure for the resonant three-wave interaction, Physica D 123(1-4), 271 (1998)

13. M. V. Berry, Quantal phase factors accompanying adiabatic changes, Proc. R. Soc. Lond. A 392(1802), 45 (1984)

14. E. Cohen, H. Larocque, F. Bouchard, F. Nejadsattari, Y. Gefen, and E. Karimi, Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond, Nat. Rev. Phys. 1(7), 437 (2019)

15. Y. Aharonov, and J. Anandan, Phase change during a cyclic quantum evolution, Phys. Rev. Lett. 58(16), 1593 (1987)

16. J. Samuel and R. Bhandari, General setting for Berry’s phase, Phys. Rev. Lett. 60(23), 2339 (1988)

17. A. Shapere and F. Wilczek, Geometric Phases in Physics, World Scientific, 1989

18. S. Pancharatnam, Generalized theory of interference, and its applications, Proc. Indian Acad. Sci. Sect. A 44(5), 247 (1956)

19. S. Ramaseshan and R. Nityananda, The interference of polarized light as an early example of Berry’s phase, Curr. Sci. 55, 1225 (1986)

20. M. V. Berry, The adiabatic phase and Pancharatnam’s phase for polarized light, J. Mod. Opt. 34(11), 1401 (1987)

21. N. Meinzer, W. L. Barnes, and I. R. Hooper, Plasmonic meta-atoms and metasurfaces, Nat. Photonics 8(12), 889 (2014)

22. H. Suchowski, D. Oron, A. Arie, and Y. Silberberg, Geometrical representation of sum frequency generation and adiabatic frequency conversion, Phys. Rev. A 78(6), 063821 (2008)

23. A. Karnieli and A. Arie, Fully controllable adiabatic geometric phase in nonlinear optics, Opt. Express 26(4), 4920 (2018)

24. H. Suchowski, G. Porat, and A. Arie, Adiabatic processes in frequency conversion, Laser Photonics Rev. 8(3), 333 (2014)

25. A. Karnieli, S. Trajtenberg-Mills, G. Di Domenico, and A. Arie, Experimental observation of the geometric phase in nonlinear frequency conversion, Optica 6(11), 1401 (2019)

26. G. Li, S. Zhang, and T. Zentgraf, Nonlinear photonic metasurfaces, Nat. Rev. Mater. 2(5), 17010 (2017)

27. L. Michaeli, S. Keren-Zur, O. Avayu, H. Suchowski, and T. Ellenbogen, Nonlinear surface lattice resonance in plasmonic nanoparticle arrays, Phys. Rev. Lett. 118(24), 243904 (2017)

28. R. Czaplicki, A. Kiviniemi, M. J. Huttunen, X. Zang, T. Stolt, I. Vartiainen, J. Butet, M. Kuittinen, O. J. F. Martin, and M. Kauranen, Less is more: Enhancement of second-harmonic generation from metasurfaces by reduced nanoparticle density, Nano Lett. 18(12), 7709 (2018)

29. G. Li, S. Chen, N. Pholchai, B. Reineke, P. W. H. Wong, E. Y. B. Pun, K. W. Cheah, T. Zentgraf, and S. Zhang, Continuous control of the nonlinearity phase for harmonic generations, Nat. Mater. 14(6), 607 (2015)

30. M. Tymchenko, J. S. Gomez-Diaz, J. Lee, N. Nookala, M. A. Belkin, and A. Alù, Gradient nonlinear pancharatnam-berry metasurfaces, Phys. Rev. Lett. 115(20), 207403 (2015)

31. O. Wolf, S. Campione, A. Benz, A. P. Ravikumar, S. Liu, T. S. Luk, E. A. Kadlec, E. A. Shaner, J. F. Klem, M. B. Sinclair, and I. Brener, Phased-array sources based on nonlinear metamaterial nanocavities, Nat. Commun. 6(1), 7667 (2015)

32. W. K. Burns and N. Bloembergen, Third-harmonic generation in absorbing media of cubic or isotropic symmetry, Phys. Rev. B 4(10), 3437 (1971)

33. S. Chen, G. Li, F. Zeuner, W. H. Wong, E. Y. B. Pun, T. Zentgraf, K. W. Cheah, and S. Zhang, Symmetry-selective third-harmonic generation from plasmonic metacrystals, Phys. Rev. Lett. 113(3), 033901 (2014)

34. C. McDonnell, J. Deng, S. Sideris, T. Ellenbogen, and G. Li, Functional THz emitters based on Pancharatnam-Berry phase nonlinear metasurfaces, Nat. Commun. 12(1), 30 (2021)

35. Y. Zhang, Y. Sheng, S. Zhu, M. Xiao, and W. Krolikowski, Nonlinear photonic crystals: From 2D to 3D, Optica 8(3), 372 (2021)

全文下载：

https://journal.hep.com.cn/fop/EN/10.1007/s11467-021-1123-4

https://journal.hep.com.cn/fop/EN/pdf/10.1007/s11467-021-1102-9

(整理：蔻享学术 & FOP)

《前沿》系列英文学术期刊

由教育部主管、高等教育出版社主办的《前沿》（Frontiers）系列英文学术期刊，于2006年正式创刊，以网络版和印刷版向全球发行。系列期刊包括基础科学、生命科学、工程技术和人文社会科学四个主题，是我国覆盖学科最广泛的英文学术期刊群，其中13种被SCI收录，其他也被A&HCI、Ei、MEDLINE或相应学科国际权威检索系统收录，具有一定的国际学术影响力。系列期刊采用在线优先出版方式，保证文章以最快速度发表。

中国学术前沿期刊网

http://journal.hep.com.cn