论文标题：Bayesian Nonparametric Inference in Elliptic PDEs: Convergence Rates and Implementation

论文链接：https://www.mdpi.com/2673-9321/5/2/14?n1=43&_utm_from=315ffb84f5

期刊名：Foundations

期刊主页：https://www.mdpi.com/journal/foundations?n1=43&_utm_from=315ffb84f5

偏微分方程（PDE）中的参数识别问题旨在确定偏微分方程中的一个或多个函数型系数。本文研究了此类问题的贝叶斯非参数方法。以从偏微分方程解的含噪观测值中推断椭圆型偏微分方程的扩散函数这一典型示例为重点，研究了基于高斯过程先验的贝叶斯方法的性能。基于文献中的最新进展，我们推导出了新的渐近理论保证，为基于狄利克雷-拉普拉斯特征基的、在方法上颇具吸引力的高斯级数先验建立了后验一致性及收敛速率。本文还提供了基于相关后验的推断的实现方法，并通过数值模拟研究对其进行了说明，模拟结果与理论高度吻合。

研究过程与结果

偏微分方程（PDEs）是模拟复杂现实世界现象行为的主要数学工具，在工程和科学领域有着普遍的应用。PDE的公式通常涉及许多功能参数，这些参数在应用中通常是未知的，并且不能直接进行测量。因此，在实际中采用偏微分方程模型需要事先从现有数据中确定方程中的参数，这就产生了参数识别的逆问题。

在本文中，我们将聚焦于以下典型示例。考虑一个物理量在具有光滑边界的非均匀多维凸区域（）内发生扩散的情形。在平衡状态下，扩散物质在任意位置处的密度u(x)由二阶椭圆型偏微分方程控制：

{∇⋅(f∇u)=s,u=b,在 O 上,在 ∂O 上,

（1）

其中，描述局部源或汇的空间分布，规定边界上的密度值，而扩散函数→(0,∞)则对整个非均匀区域内的空间变化传导率进行建模。在偏微分方程系数满足适度正则性条件的假设下，根据标准椭圆型理论，方程（1）存在唯一二阶连续可微的经典解（例如，参见文献[10]第6章）。假设s和b已知，我们的兴趣在于从G(f)在区域内（可能为随机）设计点网格X₁,…,X_n上的n个含噪点估计值中估计f，即：

Yi=G(f)(Xi)+Wi,i=1,…,n,

（2）

其中，X₁,…,X_n为统计测量误差，>0为噪声水平。根据中心极限定理，通常可以合理地假设X₁,…,X_n服从独立同分布的正态分布N(0,1)。从椭圆型偏微分方程（1）的解中恢复扩散系数的反问题是油藏建模中的一个重要组成部分（参见文献[11]），其中u为（可通过测量获取的）流体压力，而f为（无法直接观测的）渗透率场，由于油藏成分的变化，渗透率场可能表现出剧烈的空间变化。该问题在应用数学（例如，参见文献[12,13,14]）和统计学（例如，参见文献[5,15,16]）领域的大量文献中均有研究。二维区域上的示例见图1。

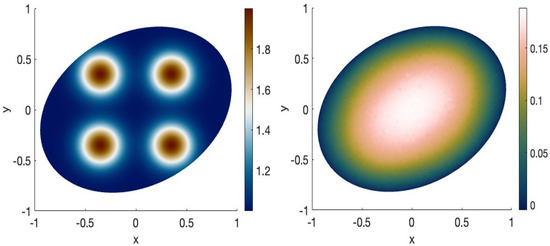
图1.（左）：一个扩散函数f的示例，其中包含四个具有更高导电性的圆形区域。（右）：从对应的偏微分方程解G(f)中获取的n=4500个含噪观测值

研究总结

在本文中，我们研究了椭圆型偏微分方程推断中的非参数贝叶斯方法，重点聚焦于通过偏微分方程解的含噪观测值来估计扩散函数这一标准基准问题。我们针对后验分布和后验均值估计量给出了一个一般性的渐近集中结果，即定理1，并表明该结果适用于两类有趣的高斯先验，即定义在狄利克雷-拉普拉斯特征基上的截断高斯级数先验（参见示例1）和马特恩（Matérn）过程先验（参见示例2）。对于这两种先验模型，我们设计了基于后验推断的实现策略，采用了高效可靠的马尔可夫链蒙特卡洛（MCMC）算法。数值模拟研究考察了所考虑方法的性能，结果表明重建效果极佳，且与理论高度吻合。总体而言，该方法的主要优势在于其建模灵活性、相关计算方法的稳健性，以及恢复性能理论保证的可用性。

最后，让我们概述一些相关研究问题。首先，我们注意到，在本文中，式（2）中的噪声标准差始终被假定为已知。在也未知的现实情形中，可借鉴经验贝叶斯的思想，用初步（非似然）估计值替换，从而轻松调整本文所开发的方法。文献中提出了多种非参数回归模型中的方差估计策略，包括基于核平滑[31]和样条[32]的残差估计量，以及基于差分的估计量[33]。或者，也可通过为设定先验分布（例如，独立的共轭逆伽马先验），来考虑式（2）中f和的联合贝叶斯模型。这引出了一个有趣的问题，即将第2节中给出的理论结果扩展到方差未知的情形；直接回归模型中的相关结果可参见[34]。

其次，我们提到了为所考虑的先验分布指定超参数值这一重要问题，即示例1中截断高斯级数先验的正则性参数，以及马特恩协方差核（16）中的平滑度和长度标度。关于经验贝叶斯和分层贝叶斯策略在完全数据驱动超参数选择中的方法论和理论方面，已有大量文献进行了研究；更多参考文献可参见[20,35,36,37,38]。研究这些方法在本文所考虑的椭圆型偏微分方程模型和高斯先验分布背景下的影响和性能，是未来研究的一个有趣方向。