导读

波粒二象性和纠缠是量子物理的基础概念，但它们的确切关系长期以来仍是个谜。上海交通大学麻志浩教授课题组联合首都师范大学/德国马普所费少明教授、文鳐科技首席科学家芮子文、新加坡科技局高级科学家肖运龙建立了一个统一波粒二象性与纠缠的理论框架。他们给出了波粒二象性与纠缠之间的守恒律，揭示了这两者之间的深层联系。北京大学王剑威教授团队已通过硅集成纳米光量子芯片进行了实验验证。

近日，相关研究成果以“Universal Conservation Laws of the Wave–Particle–Entanglement Triad: Theory and Experiment”为题发表在国际顶尖光学期刊《Light: Science & Applications》。

研究背景

光既是波也是粒子，这就是波粒二象性，也是量子力学最令人困惑的问题之一。波粒二象性是量子力学理论的基础，诺贝尔奖获得者理查德·费曼将其称为“量子力学中一个真正的奥秘”，只有理解了波粒二象性才真正理解量子力学。而量子纠缠作为一种非经典的关联，也已经在实验上得到验证。

虽然波粒二象性是量子力学中历史悠久的问题，波尔在量子力学早期就提出了互补性原理来说明波粒二象性关系，但是如何量化粒子的波动性与粒子性一直是一个难题。直到1979年，Wootters等人首次提出了波粒二象性的量化方法。随后在1996年Englert继续完善了这种量化的方法，他提出了一个不等式，即著名的波粒二象性对偶关系。

在Englert提出的双缝实验中，光子可能经过上下两条路径，通过路径后面的探测器判断光子究竟经过了哪一条路径。同时光屏上会出现明暗相间的干涉条纹，波动性与最亮和最暗的干涉条纹有关。而粒子性衡量判断粒子路径的能力，如果粒子性等于1，则表示能准确无误地判断粒子的路径。后来有学者提出了波动性与粒子性度量的公理，随后涌现出了大量相关的研究。这些研究主要关注于找到满足这些公理的度量，进而得到新的波粒二象性对偶关系。

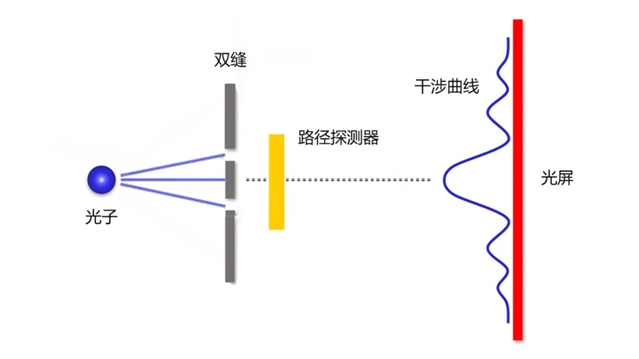
图1.双缝干涉实验示意图。

虽然找到了量化波粒二象性的方法，但同时又出现另一个问题：波粒二象性的互补关系是通过不等式刻画的，这个不等式是否是精确的，是否可以变为等式？我们希望找到波粒二象性关系中缺失的元素，使得原来的不等式能变成等式。

基于这个问题，上海交通大学麻志浩教授课题组联合首都师范大学/德国马普所费少明教授、新加坡科技局高级科学家肖运龙研究发现，波粒二象性和量子纠缠有深刻的内在联系，考虑到光子和环境纠缠的时候，光子的波动性度量、粒子性度量、光子和环境的纠缠三者的和一定是个常数。麻志浩等人提出了一个统一的理论框架可以方便地量化波动性、粒子性、量子纠缠的大小，这个框架涵盖常见的多种著名的波动性、粒子性以及纠缠度量；证明了这三个度量之间存在守恒关系。具体来说，对于一个两光子的封闭系统(两体任意维纯态)，波动性和粒子性度量，与两体纯态的量子纠缠度量之间存在互补关系，波动性、粒子性与纠缠三者之和一定是一个常数，这个常数不依赖于这个两体纯态的选择。北京大学王剑威教授团队利用硅集成纳米光量子芯片，实验上验证了这种守恒关系。

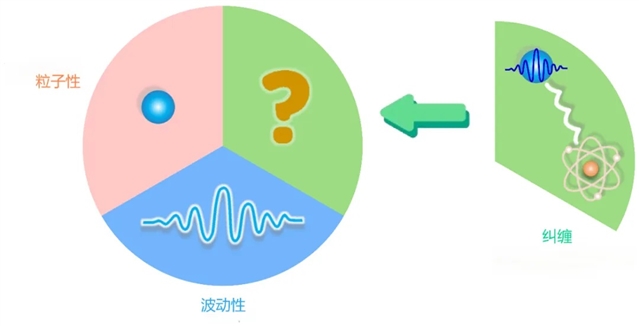
图2. 波粒二象性与纠缠间的守恒关系示意图。

创新研究

上海交通大学麻志浩教授课题组发现量子态的波动性、粒子性和纠缠度量都可以统一通过同一个可微的严格凸函数得到。通过这个凸函数的选择，就可以得到无数个合法的波动性、粒子性和纠缠的度量，这里合法指的是波动性、粒子性和纠缠的度量都满足各自对应的一些合理的公理假设。对于每一个凸函数，发现波动性、粒子性和纠缠的度量这三者之和都是一个常数，并且这个常数只依赖于维数和选取的函数。这样，我们实际上得到了无数种（而不是一种）波动性、粒子性、量子纠缠之间的等式关系，也就是这三者之间存在着守恒关系，这并不是一种数学上的巧合，而是说明这三个关键的物理量确实有内在的深刻联系，因此可以得到统一的守恒规律。

北京大学王剑威教授团队利用硅集成纳米光量子芯片验证这个理论，实验不仅仅是对量子比特系统（二维情况）进行了验证，实验验证了二维、三维和四维量子态的情形，不论量子态维数多大，实验结果均与理论高度契合，再次表明波粒二象性与纠缠间的守恒关系是普遍存在的，这也是首次对于高维量子态波粒二象性对偶关系的实验验证，之前的实验都是基于量子比特系统的实验。另一方面，对于两体混态的情形（即两体开放系统），理论上发现守恒关系不再成立，变成了不等式的关系，实验结果也验证了这一理论预测。从信息论的角度来看，这说明在开放系统中某些信息耗散到了环境中，使得总信息量减少了，从而守恒关系不再成立。

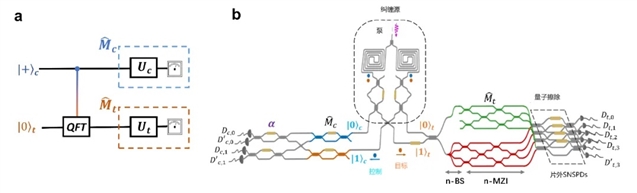
图3. a 实验线路图；b 实验装置示意图。

总结和展望

该研究提出了一个统一的理论框架，能够统一定量刻画波动性、粒子性和量子纠缠，发现三者之间的守恒关系是普遍存在的。同时实验上利用硅集成纳米光量子芯片对于高维量子系统验证了这种守恒关系。这项研究不仅加深了人们对波粒二象性和纠缠关系的理解，还推动了量子力学基础问题的深入研究，并在量子精密测量等领域发现了新的技术应用。（来源：LightScienceApplications微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-025-01759-4