论文标题： The Averaging Principle for Hilfer Fractional Stochastic Evolution Equations with Lévy Noise

论文链接：https://doi.org/10.3390/fractalfract8010003

期刊名：Fractal and Fractional

期刊主页：https://www.mdpi.com/journal/fractalfract

研究背景与动机

在科学与工程领域，随机微分方程（SDEs）应用广泛，但许多系统不仅依赖当前状态，还涉及过去状态及时滞导数，分数阶随机微分方程（FSDEs）因能刻画这一特性，在力学、电学、物理学等领域应用广泛。随机动力学主要涉及高斯噪声，纯高斯噪声因受内外部干扰难以模拟实际现象，而非高斯Lévy 噪声已经包含了扰动，且具有呈现长尾分布的优势，其重要性不容忽视。同时，Hilfer分数阶导数作为广义导数，能统一经典 Riemann-Liouville 与 Caputo 导数的特性，让模型更贴合实际场景，二者结合构建的Hilfer分数阶 Lévy 噪声随机发展方程（HFSEEs），成为描述复杂系统的重要工具。

平均原理作为简化复杂随机系统的关键方法，其价值在于 “用结构更简洁的平均方程近似替代原方程”，从而大幅降低分析难度。但是现有研究仅在有穷维空间考虑Hilfer分数阶随机微分方程（HFSDEs）的平均方法，针对这一局限，来自太原理工大学与中山大学的研究团队开展深入研究。“HFSEEs的某些平均原理在无穷维空间中是否仍然成立？如果成立，我们应该如何建立该平均原理? ”成为本文的研究动机。

研究推导与验证

本文建立了一类Hilfer分数阶随机发展方程（HFSEEs）温和解的存在唯一性定理，并在此基础上推导了所研究系统的平均原理。

1.定义空间与算子

令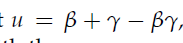定义巴拿赫空间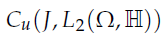，范数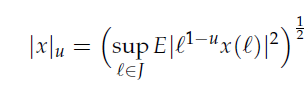，并构造有界闭凸子集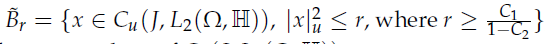

)，（C_1，C_2为推导所得常数）；同时定义算子ψ，其表达式对应文中方程（3）的积分形式如下图1，温和解等价于该算子的不动点。

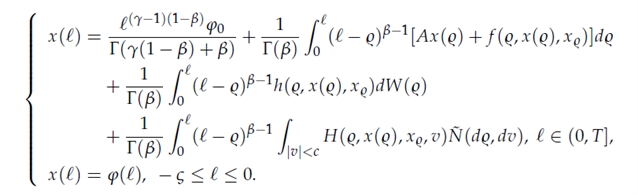
图1：文中方程（3）的积分形式

2.关键假设

对 HFSEEs 中的函数f,h,H提出假设（H1-H4）：H1-H2 分别给出f的 Lipschitz 条件与线性增长条件、h和H关于噪声项的类似条件；H3 引入凹函数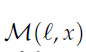约束函数差值；H4 确保平均函数(y,h,H)的收敛性。

3.温和解存在唯一性证明

通过三步推导：一是证明算子ψ在Br 上连续；二是证明ψ将Br 映射到自身；三是证明ψ为压缩映射（利用Cauchy-Schwarz 不等式、B-D-G 不等式等，证得

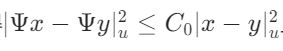,且C_0=1。结合巴拿赫不动点定理，得出方程（3）在Br 上存在唯一温和解的结论。

4.平均原理推导

引入 HFSEEs 的扰动形式（含小参数ε）及其温和解, 定义平均方程及其温和解

如下图2所示, 通过估计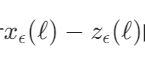的均方误差（分解为I_1,I_2,I_3,三项分别计算，结合 广义 Gronwall 不等式等，证明当ε趋近于0时， 在均方意义下收敛到; 再由 Chebyshev-Markov 不等式，证得概率意义下的收敛性。

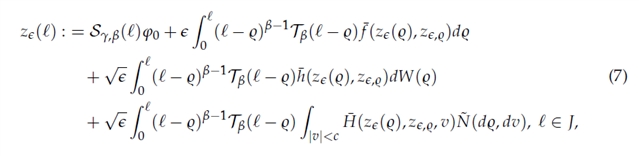
图2：平均方程的温和解

5.实例验证

为验证前文推导的Hilfer分数阶随机发展方程（HFSEEs）平均原理有效性，本文构造一维希尔伯特空间下的具体实例，结果验证了 HFSEEs 平均原理的正确性与实用性。

Fractal and Fractional 期刊介绍

主编：Carlo Cattani, University of Tuscia, Italy

期刊主题涵盖包括分形和分数阶微积分基础研究及其在不同科学和工程领域中的应用研究。现已被 SCIE (Web of Science)、Scopus 等重要数据库收录，JCR category rank: 22/136 (Q1)，中科院2区。