声子是晶格振动能量量子化的准粒子。德拜理论在历史上具有举足轻重的地位，但仅适用于线性色散声子。经典德拜理论存在两大局限性：一是范霍夫奇点（VHS），二是玻色峰（BP）。此前，关于玻色峰的物理起源及其与范霍夫奇点是否等效存在长期争议。

近日，中国科学院力学研究所研究员蒋敏强团队突破德拜理论限制，建立了考虑非线性散射效应的声子统一理论，终结了两类非德拜声子异常现象的物理关系之争。

研究团队从声子散射物理规律入手，理论推导了多自由度晶格振动的阻尼系数，以及考虑阻尼软化的声子频率-波数色散关系，实现了从低波数瑞利散射到高波数米氏散射转变的光滑描述，从而将德拜线性色散拓展至非线性空间。在声子动力学格林响应函数框架下，得到了可统一描述有序晶体和无序固体（玻璃等）的声子态密度解析表达。

在此基础上，研究团队以散射体特征尺寸和散射声子平均自由程为参数空间，构建了非德拜声子异常的全景相图。分析发现，如果声子色散呈现非线性连续软化，则玻色峰和范霍夫奇点可由同一实体演变为高度耦合且可相互转换的两个变体；如果声子强烈散射导致色散出现额外的局域共振软化，则玻色峰和范霍夫奇点可作为完全不同的现象而独立地同时涌现，两者共存的相边界可由理论精确确定。研究团队还计算了非德拜声子异常引起的低温比热行为，并得到涵盖有序晶体到无序玻璃的143个真实固体的实验数据证实，这表明建立的声子统一理论具有广泛的普适性和有效性。

上述发现不仅澄清了玻色峰的物理起源及其与范霍夫奇点的关系，还加深了对拓扑有序或无序固体连续介质弹性极限的基本理解。

相关研究成果发表在《自然-物理学》（Nature Physics）上。研究工作得到国家自然科学基金的支持。（来源：中国科学院力学研究所）

相关论文信息：https://doi.org/10.1038/s41567-025-03057-7

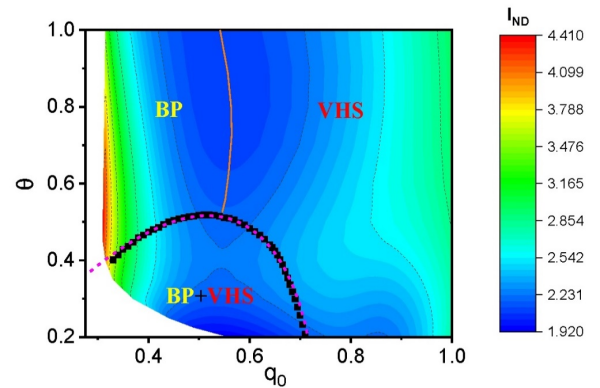
基于声子统一理论构建的非德拜异常（玻色峰和范霍夫奇点）全景相图

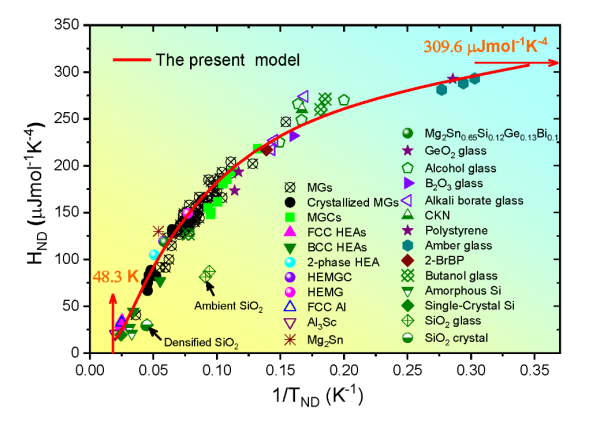
声子统一理论得到143种真实固体的低温比热数据验证