导读

近日，来自洛桑联邦理工学院的Giulia Tagliabue团队，展示了由第一性原理模拟所支持的实验证据，揭示了薄单晶金片发光过程的量子力学效应，对未来进一步探索多种材料系统中的热载流子和电荷转移动力学铺平了道路。该文章发表在国际顶尖学术期刊《Light: Science & Applications》，题为“Quantum-mechanical effects in photoluminescence from thin crystalline gold films”。

研究背景

1969年，学者们首次观察到金属发光的现象。相比于半导体发光，金属发光的光信号强度要弱几个数量级。不过，随着对等离子体纳米结构研究的兴起，这一效应近年来也越来越受到人们的关注。等离子体产生的热载流子能够显著提高局部电子温度，增强分子的弱发光过程，有望为医疗保健、传感和新能源等行业技术带来变革。

稳态发光具有揭示等离子体系统中热载流子过程的独特潜力，但与脉冲激光产生的双光子光致发光相比，该过程受到的关注较少。金属的稳态发光已被用于监测表面和电子温度、探测金分子相互作用以及监测电荷转移过程等重要研究中。然而，金属发射光的起源仍然存在不确定性，特别是它是由于电子和空穴的复合（光致发光，photoluminescence，PL）还是由其他形式的非弹性光散射导致的，一直是许多理论和实验研究的争议点。同时，这些争论因为其他效应而变的更加复杂，比如与金属结构的等离子体模式共振的特定波长光发射的珀塞尔增强（Purcell enhancement）、激发波长相对于带间跃迁阈值的位置和空间限制等效应。

在没有共振激发参与的情况下，人们对带间激发后金属的稳态发光仍然缺乏充分的了解，这阻碍了其作为有效探针的应用。因此，探究金属发光的深层原理，具有极高的学术价值和应用价值。

创新研究

在该研究中，研究人员研究了厚度为13 nm到113 nm的原子级平坦的单晶金片在（111）表面暴露下的光子发射过程。这些样品使研究人员能够在没有表面粗糙度或等离子体增强的情况下探测光子发射和纳米级限制之间的关系，因此该研究得出的结论可以普遍应用于任何金属，而不仅仅是在等离子体状态下工作的金属。该研究表明，当在带间区域照射时，长波长的光子发射与激发波长无关，表明该信号是由光致发光而不是其他形式的非弹性散射引起的。此外，研究还证明了，当在488 nm处激发时，仅使用斯托克斯信号（即波长比激发波长更长的信号）的金发光可以用作局部温度的探针（图一）。

图一：a) 测量过程示意图，包括入射激光光斑和发射光。b) 厚度为79 nm的金片在显微镜下的白光反射图像，488 nm 波长的激光入射到金片的中心部分。c) 88 nm厚的金片的光致发光，每个吸收光子归一化为关于激发波长的函数。插图展示了长波长区域的实验结果细节。对于 488 nm/532 nm/785 nm 激光激发波长，入射强度分别为 1.449 mW·μm^-2 /3.334 mW·μm^-2 /0.063 mW·μm^-2。d) i发光之前和ii光致发光过程之前无电荷弛豫的非弹性光散射示意图。光致发光涉及激发电子的散射（绿点），而非光致发光的非弹性光散射由虚态介导（虚线），在光子发射之前没有发生任何弛豫过程。e) 室温下不同激光激发功率下 113 nm 厚金片的光致发光的光谱依赖性，以及 f)恒定激发功率为 0.072 mW·μm^-2的样品温度。g) 113 nm 厚薄片的外部光致发光量子产率关于激发功率的函数。在 e)-g) 中，激发波长为 488 nm，灰色阴影区域对应于定义的“短λ_out”范围。

为了进一步了解光发射过程，该研究采用光子重吸收，揭示了在光子发射之前的光激发之后存在最小的电荷扩散（图二）。

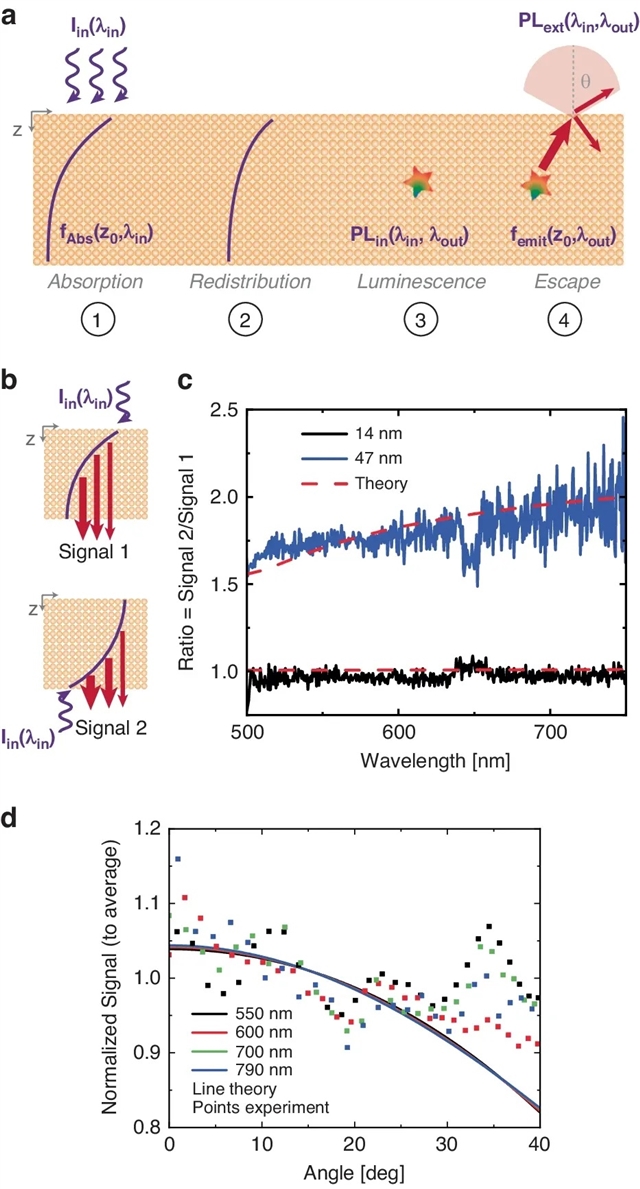
图二：a) 光子吸收后发生的过程示意图。b) 测量方法示意图 – 从上方和下方激发金片，并记录光致发光信号两次测量中的相同底面（分别为信号 1 和信号 2）。c) 子图b)中所示的两个信号之间的比率的波长依赖性，以及假设光致发光发射发生在产生电荷的位置的计算。图中展示了47 nm和14 nm厚度的薄片的结果。对于激励和收集同侧以及异侧的情况，激励功率分别为0.057 mW·μm^-2和0.057 mW·μm^-2。信号被归一化为入射光子的数量。d)在 厚度为88 nm的薄片上进行 激发强度为0.604 mW·μm^-2 的488 nm激发时，550 nm、600 nm、700 nm 和 790 nm (±10 nm) 发射波长下的角度分辨发光（归一化为平均值）以及预测的角度依赖性。

基于此，研究人员提出一个发光模型，其中包括光子重吸收和基于密度泛函理论 (DFT) 的第一性原理计算，产生的结果与 PL实验非常吻合（图三）。

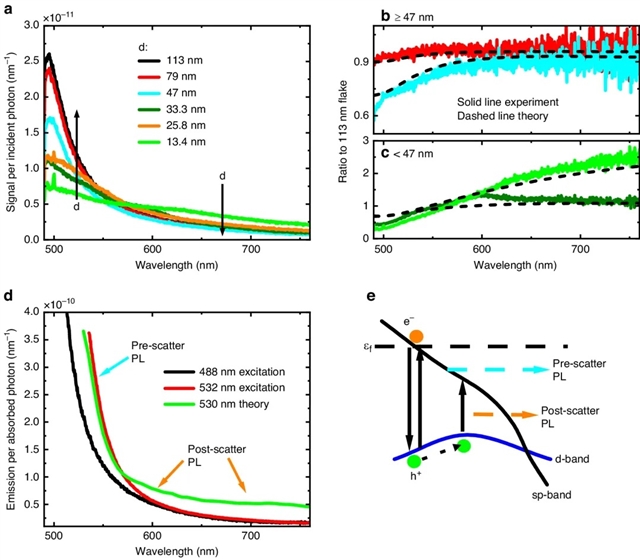
图三：a) 在 488 nm 激发波长下记录的不同薄片厚度 d 的每个入射光子的光致发光。b, c) 子图a) 中的测量信号与从厚度为113 nm的薄片获得的信号之比，并分别分为 b) 厚薄片和 c) 薄薄片。虚线为该研究提供的模型计算出的轮廓。b) 和 c) 中的曲线颜色与 a) 保持一致。d) 计算 488 nm 和 532 nm 光激发的内部发光（使用 88 nm 厚的薄片数据），以及模拟 530 nm 波长激发的内部发光。e) 光致发光过程示意图，其中εf 表示费米能量，h⁺ /e ^- 表示光激发后激发的空穴/电子。在所有子图中，对于 488 nm和532 nm激发波长，样品上的入射激光功率分别为 0.162 mW·μm^-2 和3.334 mW·μm^-2。

金的PL（当在带间区域激发时）由两个关键成分组成，两者都是由激发的 d 带空穴与未激发的电子复合产生的：接近激发能量的预散射发光和较长波长的后散射发光。该研究提出的体发光模型表明，当薄片厚度减小到 40 nm 以下时，费米能级附近的量子力学状态限制会导致较长波长下的预散射发光增加（与厚度较高的薄片相比）， 并通过第一性原理建模证明了这一点（图四）。

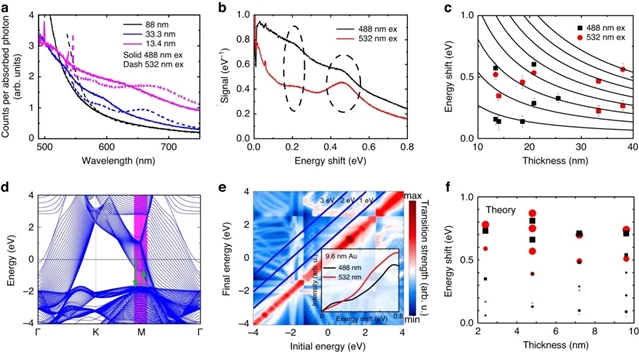
图四：a）用488 nm和532 nm波长光（激发强度分别为0.322 mW·μm^-2和0.549 mW·μm^-2）激发后，厚度为88 nm、33.3 nm和13.4 nm的薄片的归一化发光信号。b) 厚度为33.3 nm的薄片的发光信号关于488 nm (1.449 mW·μm^-2 ) 和 532 nm (3.334 mW·μm^-2 ) 激发波长能量位移的函数。c) 488 nm（黑色方块）和 532 nm（红色圆圈）的共振峰能量位移关于样品厚度的函数。d) Au (111) 40 个原子层的电子能带色散。布里渊区 M 点附近由粉色区域表示，预散射发光过程覆盖在绿色箭头中，表示空穴的激发和随后的弛豫。e) 40 个 Au (111) 原子层的偶极矩阵元在如 d) 所示的布里渊区的粉红色区域上的平均值关于初始和最终状态能量的函数。使用偶极矩阵元素估计的发光强度在插图中展示为关于 488 nm 和 532 nm 激发能量偏移的函数。f) 预测强度的变化（黑色方块和红色圆圈的大小表示作为 e) 中插图的光谱中的特征出现的相应跃迁的强度）以及从第一原理计算获得的共振峰的能量偏移关于金膜厚度的函数。

最后，该研究探索了在带内状态下激发时的发光信号。通过调用标度论证，研究人员提出带内发光实际上不仅仅归因于光致发光。该研究结果提供了单晶薄片中金光致发光的综合理论，该理论很容易适用于其他金属和纳米颗粒。

结论与展望

该研究解决了近50年来关于金发光起源的争论，对等离子体物理学的进步具有重要的意义，同时也为基于金属发光的进一步研究和应用铺平了道路。（来源：LightScienceApplications微信公众号）

相关论文信息：https://doi.org/10.1038/s41377-024-01408-2